# 线段树模板

# 一、线段树基本概念

1、线段树是一颗二叉树，储存的是一个区间的信息，每个节点都是一个结构体，结构体里面包含区间左端点，区间右端点，区间所需要维护的信息

2、线段树基本思想是二分

3、线段树一般结构如下图

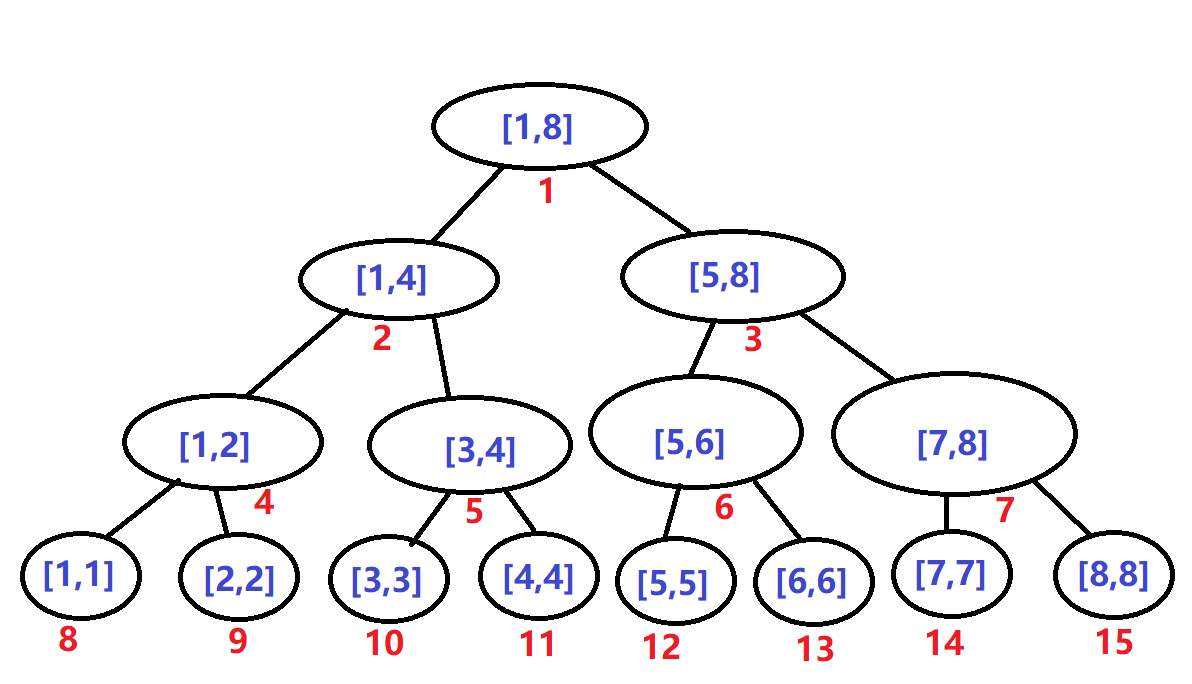
本人线段树一般书写方法不太一样，如下：

Code:

struct node
{
    int l,r,left_child,right_child;
    int sum,delay;
}tree[N*2]; //线段树每一个节点结构体

int root,tot,d[N];

void push_up(root) //合并操作
{
    int a=tree[root].left_child,b=tree[root].right_child;
    tree[root].sum=tree[a].sum+tree[b].sum;
    tree[root].sum+=(tree[a].r-tree[a].l+1)*tree[a].delay,tree[root].sum+=(tree[b].r-tree[b].l+1)*tree[b].delay;
    return;
}

void build(int & root,int l,int r) //建树
{
    root=++tot,tree[root].l=l,tree[root].r=r;
    if(l==r)
    {
        tree[root].sum=d[l];
        return;
    }
    int mid=(l+r)>>1;
    build(tree[root].left_child,l,mid);
    build(tree[root].right_child,mid+1,r);
    push_up(root);
    return;
}

void push_down(int root) //修改时将延迟标记落实
{
    int a=tree[root].left_child,b=tree[root].right_child;
    if(tree[root].delay)
    {
        tree[a].sum+=(tree[a].r-tree[a].l+1)*tree[root].delay,tree[a].delay+=tree[root].delay;
        tree[b].sum+=(tree[b].r-tree[b].l+1)*tree[root].delay,tree[b].delay+=tree[root].delay;
        tree[root].delay=0;
    }
    return;
}

void update(int root,int l,int r,int v) //区间修改
{
    if(l<=tree[root].l && tree[root].r<=r)
    {
        tree[root].delay+=v;
        return;
    }
    push_down(root);
    int mid=(tree[root].l+tree[root].r)>>1;
    if(mid>=r)
        update(tree[root].left_child,l,r,v);
    else if(mid<l)
        update(tree[root].right_child,l,r,v);
    else
        update(tree[root].left_child,l,mid,v),update(tree[root].right_child,mid+1,r,v);
    push_up(root);
    return;
}

int query(int root,int l,int r) //区间查询
{
    if(l<=tree[root].l && tree[root].r<=r)
        return tree[root].sum;
    push_down(root);
    int mid=(tree[root].l+tree[root].r)>>1;
    if(mid>=r)
        return query(tree[root].left_child,l,r);
    else if(mid<l)
        return query(tree[root].right_child,l,r);
    else
        return query(tree[root].left_child,l,mid)+query(tree[root].right_child,mid+1,r);
}

void change(int root,int id,int v) //单点修改
{
    if(tree[root].l==tree[root].r)
    {
        tree[root].sum+=v;
        return;
    }
    int mid=(tree[root].l+tree[root].r)>>1;
    push_down(root);
    if(mid>=id)
        change(tree[root].left_child,l,r);
    else
        change(tree[root].right_child,l,r);
    push_up(root);
    return;
}

# 二、线段树板子（包含区间求和，单点修改，区间修改）

例题：线段树模板 1

例题：线段树模板 2

#include <bits/stdc++.h>
using namespace std;
const long long N=100001;
struct node
{
	long long l,r,left_child,right_child;
	long long sum,delay1,delay2;
}tree[N*2];
long long n,m,root,tot,d[N],mod;
void fix(long long root)
{
	long long a=tree[root].left_child,b=tree[root].right_child;
	tree[root].sum=tree[a].sum+tree[b].sum;
	tree[root].sum%=mod;
	return;
}
void build(long long & root,long long l,long long r)
{
	root=++tot,tree[root].l=l,tree[root].r=r;
	tree[root].delay2=1;
	if(l==r)
	{
		tree[root].sum=d[l];
		return;
	}
	long long mid=(l+r)/2;
	build(tree[root].left_child,l,mid);
	build(tree[root].right_child,mid+1,r);
	fix(root);
	return;
}
void push_down(long long root)
{
	long long a=tree[root].left_child,b=tree[root].right_child;
    tree[a].sum*=tree[root].delay2,tree[a].sum+=(tree[a].r-tree[a].l+1)*tree[root].delay1;
    tree[a].delay1=tree[a].delay1*tree[root].delay2+tree[root].delay1,tree[a].delay2*=tree[root].delay2;
    tree[a].delay1%=mod,tree[a].delay2%=mod,tree[a].sum%=mod;
    tree[b].sum*=tree[root].delay2,tree[b].sum+=(tree[b].r-tree[b].l+1)*tree[root].delay1;
    tree[b].delay1=tree[b].delay1*tree[root].delay2+tree[root].delay1,tree[b].delay2*=tree[root].delay2;
    tree[b].delay1%=mod,tree[b].delay2%=mod,tree[b].sum%=mod;
    tree[root].delay1=0,tree[root].delay2=1,tree[root].sum%=mod;
    return;
}
void update(long long root,long long l,long long r,long long v)
{
	if(l<=tree[root].l && tree[root].r<=r)
	{
		tree[root].sum+=(tree[root].r-tree[root].l+1)*v;
		tree[root].delay1+=v;
		return;
	}
	push_down(root);
	long long mid=(tree[root].l+tree[root].r)/2;
	if(mid>=r)
		update(tree[root].left_child,l,r,v);
	else if(mid<l)
		update(tree[root].right_child,l,r,v);
	else
		update(tree[root].left_child,l,mid,v),update(tree[root].right_child,mid+1,r,v);
	fix(root);
	return;
}
void change(long long root,long long l,long long r,long long v)
{
	if(l<=tree[root].l && tree[root].r<=r)
	{
		tree[root].sum*=v,tree[root].delay1*=v,tree[root].delay2*=v;
		tree[root].sum%=mod,tree[root].delay1%=mod,tree[root].delay2%=mod;
		return;
	}
	push_down(root);
	long long mid=(tree[root].l+tree[root].r)/2;
	if(mid>=r)
		change(tree[root].left_child,l,r,v);
	else if(mid<l)
		change(tree[root].right_child,l,r,v);
	else
		change(tree[root].left_child,l,mid,v),change(tree[root].right_child,mid+1,r,v);
	fix(root);
	return;
}
long long query(long long root,long long l,long long r)
{
	if(l<=tree[root].l && tree[root].r<=r)
		return tree[root].sum%mod;
	long long mid=(tree[root].l+tree[root].r)/2;
	push_down(root);
	if(mid>=r)
		return query(tree[root].left_child,l,r)%mod;
	else if(mid<l)
		return query(tree[root].right_child,l,r)%mod;
	else
		return query(tree[root].left_child,l,mid)%mod+query(tree[root].right_child,mid+1,r)%mod;
}
int main()
{
	scanf("%lld %lld %lld",&n,&m,&mod);
	for(long long i=1;i<=n;i++)
		scanf("%lld",&d[i]);
	build(root,1,n);
	for(long long i=1;i<=m;i++)
	{
		long long op;
		scanf("%lld",&op);
		if(op==1)
		{
			long long l,r,x;
			scanf("%lld %lld %lld",&l,&r,&x);
			change(root,l,r,x);
		}
		else if(op==2)
		{
			long long l,r,x;
			scanf("%lld %lld %lld",&l,&r,&x);
			update(root,l,r,x);
		}
		else
		{
			long long l,r;
			scanf("%lld %lld",&l,&r);
			printf("%lld\n",query(root,l,r)%mod);
		}
	}
	return 0;
}

线段树还可以进行其他操作，如区间最大、小值等功能，这些功能待补充

# 三、可持久化线段树

光看标题不明所以，其主要功能是可以求区间任意第 k 小的值，k 是可输入改变的

例题：可持久化线段树

Code:

#include <bits/stdc++.h>
using namespace std;
const int N=200001;
struct node
{
	int left,right,sum;
}tree[20*N];
struct edge
{
	int v,old,new_id;
	bool operator < (const edge & ot) const
	{
		return v<ot.v;
	}
}d[N];
int n,m,root[20*N],tot=1;
void update(int & now,int l,int r,int pos)
{
	tree[tot++]=tree[now];
	now=tot-1;
	tree[now].sum++;
	if(l==r)
		return;
	int mid=(l+r)/2;
	if(pos<=mid)
		update(tree[now].left,l,mid,pos);
	else
		update(tree[now].right,mid+1,r,pos);
	return;
}
int query(int last,int now,int l,int r,int pos)
{
	int sum=tree[tree[now].left].sum-tree[tree[last].left].sum;
	if(l==r)
		return l;
	int mid=(l+r)/2;
	if(pos<=sum)
		return query(tree[last].left,tree[now].left,l,mid,pos);
	else
		return query(tree[last].right,tree[now].right,mid+1,r,pos-sum);
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&d[i].v),d[i].old=i;
	sort(d+1,d+1+n);
	for(int i=1;i<=n;i++)
		d[d[i].old].new_id=i;
	for(int i=1;i<=n;i++)
	{
		root[i]=root[i-1];
		update(root[i],1,n,d[i].new_id);
	}
	for(int i=1;i<=m;i++)
	{
		int l,r,k;
		scanf("%d %d %d",&l,&r,&k);
		printf("%d\n",d[query(root[l-1],root[r],1,n,k)].v);
	}
	return 0;
}

# 四、普通平衡树

普通平衡树是一颗二叉树，特点是可以动态插入删除，也可以动态查询某个数的排名及其前驱和后继

例题：普通平衡树

Code:

#include <bits/stdc++.h>
using namespace std;
const int N=100001;
int ch[N][2],par[N],size[N],cnt[N],val[N],n,tot,root;
bool flag[N];
int chk(int x) 
{
	if(ch[par[x]][1]==x)  
		return 1;
	else
		return 0;
}
void push_up(int x) 
{
	size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
	return;
}
void rotate(int cur)
{
	int x=par[cur],y=par[par[cur]],k=chk(cur);
	int which=ch[cur][k^1]; 
	ch[x][k]=which,par[which]=x; 
	ch[y][chk(x)]=cur,par[cur]=y;
	ch[cur][k^1]=x,par[x]=cur;
	push_up(x),push_up(cur);
	return;
}
void splay(int cur,int aim=0)
{
	while(par[cur]!=aim)
	{
		int x=par[cur],y=par[par[cur]];
		if(y!=aim)
		{
			if(chk(cur)==chk(x))
				rotate(x);
			else
				rotate(cur);
		}
		rotate(cur);
	}
	if(!aim)
		root=cur;
	return;
}
void insert(int x)
{
	int cur=root,fa=0;
	while(cur && val[cur]!=x)
	{
		fa=cur;
		if(x>val[cur]) 
			cur=ch[cur][1];  
		else
			cur=ch[cur][0];
	}
	if(cur)
		cnt[cur]++;
	else 
	{
		cur=++tot;
		if(fa) 
		{
			if(x>val[fa]) 
				ch[fa][1]=cur;
			else
				ch[fa][0]=cur;
		}
		ch[cur][0]=ch[cur][1]=0,par[cur]=fa,val[cur]=x,cnt[cur]=size[cur]=1; 
	}
	splay(cur); 
	return;
}
void pushdown(int x)
{
	if(flag[x])
	{
		swap(ch[x][0],ch[x][1]);
		flag[ch[x][0]]=!flag[ch[x][0]];
		flag[ch[x][1]]=!flag[ch[x][1]];
		flag[x]=false;
	}
	return;
}
int kth(int x)
{
	int cur=root;
	for(;;)
	{
		if(ch[cur][0] && x<=size[ch[cur][0]])
			cur=ch[cur][0];
		else if(x>size[ch[cur][0]]+cnt[cur])
		{
			x-=size[ch[cur][0]]+cnt[cur];
			cur=ch[cur][1];
		}
		else
			return cur;
	}
	return cur;
}
void update(int x,int y)
{
	int t1=kth(x),t2=kth(y+2);
	splay(t1),splay(t2,t1);
	flag[ch[t2][0]]=!flag[ch[t2][0]];
	return;
}
void find(int x)
{
	int cur=root;
	while(ch[cur][x>val[cur]] && val[cur]!=x)
		cur=ch[cur][x>val[cur]];
	splay(cur);
	return;
}
int pre(int x)
{
	find(x);
	if(val[root]<x)
		return root;
	int cur=ch[root][0];
	while(ch[cur][1])
		cur=ch[cur][1];
	return cur;
}
int succ(int x)
{
	find(x);
	if(val[root]>x)
		return root;
	int cur=ch[root][1];
	while(ch[cur][0])
		cur=ch[cur][0];
	return cur;
}
void print(int x)
{
	pushdown(x);
	if(ch[x][0])
		print(ch[x][0]);
	if(val[x] && val[x]<=n)
		printf("%d ",val[x]);
	if(ch[x][1])
		print(ch[x][1]);
	return;
}
void del(int x)
{
	int last=pre(x),next=succ(x);
	splay(last),splay(next,last);
	int cut=ch[next][0];
	if(cnt[cut]>1)
	{
		cnt[cut]--;
		splay(cut);
	}
	else
		ch[next][0]=0,push_up(next),push_up(root);
	return;
}
int main()
{
	scanf("%d",&n);
	insert(0x7f7f7f7f),insert(0xcfcfcfcf);
	while(n--)
	{
		int op,x;
		scanf("%d %d",&op,&x);
		if(op==1)
			insert(x);
		else if(op==2)
			del(x);
		else if(op==3)
		{
			find(x);
			printf("%d\n",size[ch[root][0]]);
		}
		else if(op==4)
			printf("%d\n",val[kth(x+1)]);
		else if(op==5)
			printf("%d\n",val[pre(x)]);
		else
			printf("%d\n",val[succ(x)]);
	}
	return 0;
}

这篇文章只是单纯的模板记录文章，要想了解原理请移步另一篇文章

下面是二叉平衡树的应用，利用二叉平衡树来维护一个有序序列

例题：文艺平衡树

Code:

#include <bits/stdc++.h>
using namespace std;
const int N=100001;
int ch[N][2],par[N],size[N],cnt[N],val[N],n,m,tot,root;
bool flag[N];
int chk(int x)//查询子节点在父节点左边还是右边 
{
	if(ch[par[x]][1]==x)  
		return 1;
	else
		return 0;
}
void push_up(int x) //更新此节点的size 
{
	size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
	return;
}
void rotate(int cur)
{
	int x=par[cur],y=par[par[cur]],k=chk(cur),which=ch[cur][k^1]; 
	//x为此节点的父亲，y为此节点的爷爷 
	ch[x][k]=which,par[which]=x; //父亲的儿子改成 
	ch[y][chk(x)]=cur,par[cur]=y;
	ch[cur][k^1]=x,par[x]=cur;
	push_up(x),push_up(cur);
	return;
}
void splay(int cur,int aim=0)
{
	while(par[cur]!=aim)
	{
		int x=par[cur],y=par[par[cur]];
		if(y!=aim)
		{
			if(chk(cur)==chk(x))
				rotate(x);
			else
				rotate(cur);
		}
		rotate(cur);
	}
	if(!aim)
		root=cur;
	return;
}
void insert(int x)
{
	int cur=root,fa=0;
	while(cur && val[cur]!=x) //当树不为空且这个点的值不是插入值 
	{
		fa=cur;//更新father 
		if(x>val[cur]) //这个值大于当前节点值 
			cur=ch[cur][1]; //右儿子 
		else
			cur=ch[cur][0]; //左二子 
	}
	if(cur) //出循环还没到底部，说明已经有这个值 
		cnt[cur]++;
	else //新建节点 
	{
		cur=++tot;
		if(fa) //如果这个点不是第一个点 
		{
			if(x>val[fa]) //同上 
				ch[fa][1]=cur;
			else
				ch[fa][0]=cur;
		}
		ch[cur][0]=ch[cur][1]=0,par[cur]=fa,val[cur]=x,cnt[cur]=size[cur]=1;//新节点信息 
	}
	splay(cur); //平衡一下 
	return;
}
void pushdown(int x)
{
	if(flag[x])
	{
		swap(ch[x][0],ch[x][1]);
		flag[ch[x][0]]=!flag[ch[x][0]];
		flag[ch[x][1]]=!flag[ch[x][1]];
		flag[x]=false;
	}
	return;
}
int kth(int x)
{
	int cur=root;
	for(;;)
	{
		pushdown(cur);
		if(ch[cur][0] && x<=size[ch[cur][0]])
			cur=ch[cur][0];
		else if(x>size[ch[cur][0]]+cnt[cur])
		{
			x-=size[ch[cur][0]]+cnt[cur];
			cur=ch[cur][1];
		}
		else
			return cur;
	}
	return cur;
}
void update(int x,int y)
{
	int t1=kth(x),t2=kth(y+2);
	splay(t1),splay(t2,t1);
	flag[ch[t2][0]]=!flag[ch[t2][0]];
	return;
}
void find(int x)
{
	int cur=root;
	while(ch[cur][x>val[cur]] && val[cur]!=x)
		cur=ch[cur][x>val[cur]];
	splay(cur);
	return;
}
int pre(int x)
{
	find(x);
	if(val[root]>x)
		return root;
	int cur=ch[root][0];
	while(ch[cur][1])
		cur=ch[cur][1];
	return cur;
}
int succ(int x)
{
	find(x);
	if(val[root]<x)
		return root;
	int cur=ch[root][1];
	while(ch[cur][0])
		cur=ch[cur][1];
	return cur;
}
void print(int x)
{
	pushdown(x);
	if(ch[x][0])
		print(ch[x][0]);
	if(val[x] && val[x]<=n)
		printf("%d ",val[x]);
	if(ch[x][1])
		print(ch[x][1]);
	return;
}
void del(int x)
{
	int last=pre(x),next=succ(x);
	splay(last),splay(next,last);
	int cut=ch[next][0];
	if(cnt[cut]>1)
	{
		cnt[cut]--;
		splay(cut);
	}
	else
		ch[next][0]=0,push_up(next),push_up(root);
	return;
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=0;i<=n+1;i++)
		insert(i);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		update(x,y);
	}
	print(root);
	return 0;
}

# 五、树链剖分

树链剖分是为了对树上进行区间修改而发明的算法，很长，很难写，但应用很多

例题：重链剖分

Code:

#include <cstdio>
#include <cstdlib>
#include <vector>
using namespace std;
const int N=100001;
struct data
{
    int h;
    int zson;
    int fa,top;
    int size;
    int tid;
}d[N];
struct node
{
    int l,r,left_child,right_child;
    int sum,delay;
}tree[N*3];
int rnk[N],n,m,R,mod,a[N],cnt=1,root,tot;
vector <int > v[N];
void dfs1(int pre,int cur)
{
    d[cur].h=d[pre].h+1;
    d[cur].fa=pre,d[cur].zson=-1;
    d[cur].size=1;
    int size=v[cur].size();
    for(int i=0;i<size;i++)
    {
        int t=v[cur][i];
        if(t!=pre)
        {
            dfs1(cur,t);
            d[cur].size+=d[t].size;
            if(d[cur].zson==-1 || d[t].size>d[d[cur].zson].size)
            d[cur].zson=t;
        }
    }
    return;
}
void dfs2(int cur,int t)
{
    d[cur].top=t;
    d[cur].tid=cnt;
    rnk[cnt]=cur;
    cnt++;
    if(d[cur].size==1 || d[cur].zson==-1)
    return;
    dfs2(d[cur].zson,t);
    int size=v[cur].size();
    for(int i=0;i<size;i++)
    {
        int x=v[cur][i];
        if(x!=d[cur].fa && x!=d[cur].zson)
        dfs2(x,x);
    }
    return;
}
void MOD(int root)
{
    tree[root].sum%=mod,tree[root].delay%=mod;
    return;
}
void fix(int root)
{
    int a=tree[root].left_child,b=tree[root].right_child;
    if(a!=-1 && b!=-1)
    tree[root].sum=tree[a].sum+tree[b].sum;
    MOD(root);
    return;
}
void build(int & root,int l,int r)
{
    root=tot++;
    tree[root].l=l,tree[root].r=r;
    tree[root].left_child=tree[root].right_child=-1;
    tree[root].delay=0;
    if(l==r)
    tree[root].sum=a[rnk[l]];
    else
    {
        int mid=(l+r)/2;
        build(tree[root].left_child,l,mid);
        build(tree[root].right_child,mid+1,r);
        fix(root);
    }
    return;
}
void push_down(int root)
{
    if(tree[root].delay!=0)
    {
        int a=tree[root].left_child,b=tree[root].right_child;
        if(a==-1 || b==-1)
        return;
        tree[a].sum+=(tree[a].r-tree[a].l+1)*tree[root].delay;
        tree[a].delay+=tree[root].delay,tree[b].delay+=tree[root].delay;
        tree[b].sum+=(tree[b].r-tree[b].l+1)*tree[root].delay;
        tree[root].delay=0;
        MOD(root);
    }
    return;
}
void update(int root,int l,int r,int v)
{
    if(l<=tree[root].l && tree[root].r<=r)
    {
        tree[root].sum+=(tree[root].r-tree[root].l+1)*v;
        tree[root].delay+=v;
    }
    else
    {
        push_down(root);
        int mid=(tree[root].l+tree[root].r)/2;
        if(mid>=r)
        update(tree[root].left_child,l,r,v);
        else if(mid<l)
        update(tree[root].right_child,l,r,v);
        else
        {
            update(tree[root].left_child,l,mid,v);
            update(tree[root].right_child,mid+1,r,v);
        }
        fix(root);
    }
    return;
}
void update_zdl(int x,int y,int z)
{
    int a=d[x].top,b=d[y].top;
    while(a!=b)
    {
        if(d[a].h>d[b].h)
        {
            update(root,d[a].tid,d[x].tid,z);
            x=d[a].fa;
        }
        else
        {
            update(root,d[b].tid,d[y].tid,z);
            y=d[b].fa;
        }
        a=d[x].top,b=d[y].top;
    }
    if(x!=y)
    {
        if(d[x].tid<d[y].tid)
        update(root,d[x].tid,d[y].tid,z);
        else
        update(root,d[y].tid,d[x].tid,z);
    }
    else
    update(root,d[x].tid,d[y].tid,z);
    return;
}
int get_ans(int root,int l,int r)
{
    if(l<=tree[root].l && tree[root].r<=r)
    return tree[root].sum;
    else
    {
        push_down(root);
        int mid=(tree[root].l+tree[root].r)/2;
        if(mid>=r)
        return get_ans(tree[root].left_child,l,r)%mod;
        else if(mid<l)
        return get_ans(tree[root].right_child,l,r)%mod;
        return (get_ans(tree[root].left_child,l,mid)+get_ans(tree[root].right_child,mid+1,r))%mod;
    }
}
int get_ans_zdl(int x,int y)
{
    int ans=0;
    int a=d[x].top,b=d[y].top;
    while(a!=b)
    {
        if(d[a].h>d[b].h)
        {
            ans+=get_ans(root,d[a].tid,d[x].tid);
            x=d[a].fa;
        }
        else
        {
            ans+=get_ans(root,d[b].tid,d[y].tid);
            y=d[b].fa;
        }
        a=d[x].top,b=d[y].top;
    }
    if(x!=y)
    {
        if(d[x].tid<d[y].tid)
        ans+=get_ans(root,d[x].tid,d[y].tid);
        else
        ans+=get_ans(root,d[y].tid,d[x].tid);
    }
    else
    ans+=get_ans(root,d[x].tid,d[y].tid);
    return ans%mod;
}
int main()
{
    scanf("%d %d %d %d",&n,&m,&R,&mod);
    for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);
    for(int i=1;i<n;i++)
    {
        int a,b;
        scanf("%d %d",&a,&b);
        v[a].push_back(b),v[b].push_back(a);
    }
    d[0].h=0,d[0].fa=-1;
    dfs1(0,R);
    dfs2(R,R);
    build(root,1,n);
    for(int i=1;i<=m;i++)
    {
        int op,x,y,z;
        scanf("%d",&op);
        if(op==1)
        {
            scanf("%d %d %d",&x,&y,&z);
            update_zdl(x,y,z);
        }
        else if(op==2)
        {
            scanf("%d %d",&x,&y);
            printf("%d\n",get_ans_zdl(x,y));
        }
        else if(op==3)
        {
            scanf("%d %d",&x,&z);
            update(root,d[x].tid,d[x].tid+d[x].size-1,z);
        }
        else
        {
            scanf("%d",&x);
            printf("%d\n",get_ans(root,d[x].tid,d[x].tid+d[x].size-1));
        }
    }
    return 0;
}

和二叉平衡树一样，本篇只做记录，不做详解，详解请移步另一篇文章