深度学习复习 - 机器学习 | Flüstern = Whispering's Blog = 无需过去，无关未来，只有现在

深度学习复习

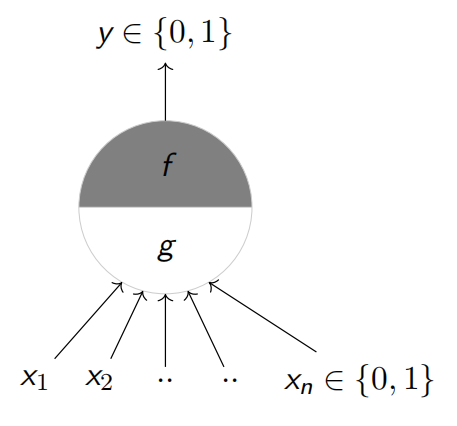
# M-P 神经元

M-P神经元

函数 g 对输入进行聚合，函数 f 基于聚合值做出一个决策

$g(x_1,x_2,...,x_n)=\sum\limits_{i=1}^nx_i$

$y=f(g(x))=\begin{cases}1&if\ g(x)\ge\theta\\0&if\ g(x)<\theta\end{cases}$

其中 $\theta$ 是阈值参数

总结：
- 一个单个的 M-P 神经元能够用来实现线性可分的布尔函数
- 对于布尔函数而言，线性可分意味着：存在一条直线或一个平面使得所有产生输出 1 的输入位于线 (或平面) 的一侧，所有产生输出 0 的输入位于线 (或平面) 的另一侧

# Perception (感知机)

感知机

$y=\begin{cases}1&if\ \sum\limits_{i=0}^nw_i*x_i\ge0\\0&if\ \sum\limits_{i=0}^nw_i*x_i<0\end{cases}$

单独一个感知机只能用于实现线性可分的函数
感知机与 M-P 神经元的差别：
- 感知机的权重包括阈值能通过学习得到
- 感知机的输入可以是实数
感知机学习算法：
$\text{Algorithm}:$ 感知机学习算法 (Perception Learning Algorithm)
$P\leftarrow$ inputs with label 1;
$N\leftarrow$ inputs with label 0;
Initialize w randomly;
while !convergence do
$\text{Pick random}\ x\in P\cup N;$
$if\ x\in P\ and\ \sum_{i=0}^nw_i*x_i<0\ then$
$w=w+x$
$end$
$if\ x\in N\ and\ \sum_{i=0}^nw_i*x_i\ge0\ then$
$w=w-x$
$end$

定理：任何有 n 个输入的布尔函数能够由一个感知机网络实现，该网络包含一个有 $2^n$ 个感知机的隐含层和一个有一个感知机的输出层

多层感知机
- 由一个输入层、一个输出层 (一个感知机模型)、一个或多个隐含层 (多个感知机模型) 构成的网络称作多层感知机 (MLP)
- 具有一层隐含层的 MLP 能够表示任意布尔函数

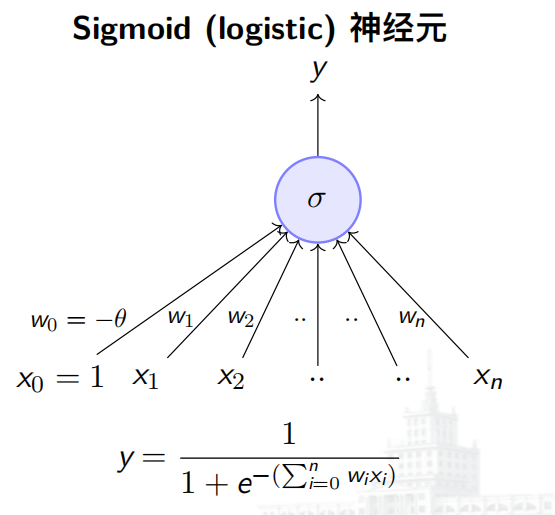
# Sigmoid 神经元

Sigmoid神经元

一个典型的有监督机器学习设置包括以下部分：

数据 (Data)： ${\{}x_i,y_i{\}}_{i=1}^n$
模型 (Model)：描述 x 和 y 之间关系的函数，例如：
- $\hat{y}=\frac{1}{1+e^{-(w^Tx)}}$
- or $\hat{y}=w^Tx$
- or $\hat{y}=x^Twx$
- 或者是任意函数
参数 (Parameters)：在所有上面的例子中，w 是需要从数据中学习的参数
学习算法 (Learning algorithm)：学习模型参数 w 的算法，例如感知机学习算法、梯度下降算法等
目标 / 损失 / 误差函数 (Objective/Loss/Error function)：用于指导学习算法 —— 学习算法的目标是最小化损失函数

梯度下降规则：

移动的方向 u 应该是与梯度的方向相差 180°
即沿着梯度的反方向移动

参数更新公式：

$w_{t+1}=w_t-\eta\nabla w_t$

$b_{t+1}=b_t-\eta\nabla b_t$

$\text{where},\nabla w_t=\frac{\delta\varphi(w,b)}{\delta w},\nabla b=\frac{\delta\varphi(w,b)}{\delta b}_{at\ w=w_t,b=b_t}$

假设有一个训练数据 (x,y)

$\varphi(w,b)=\frac{1}{2}*(f(x)-y)^2$

$\nabla w=\frac{\delta}{\delta w}[\frac{1}{2}*(f(x)-y)^2]=(f(x)-y)*f(x)*(1-f(x))*x$

$\frac{\delta}{\delta w}(\frac{1}{1+e^{-(wx+b)}})=f(x)*(1-f(x))*x$

若有多个数据

$\nabla w=\sum\limits_{i=1}^n(f(x_i)-y_i)*f(x_i)*(1-f(x_i))*x_i$

$\nabla b=\sum\limits_{i=1}^n(f(x_i)-y_i)*f(x_i)*(1-f(x_i))$

梯度下降代码：

	def do_gradient_descent():
	w,b,eta,max_epochs=-2,-2,1.0,1000
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	w-=eta*dw
	b-=eta*db

多层感知机网络的表示能力 vs 多层 Sigmoid 神经元网络的表示能力：

多层感知机神经网络：有一个隐含层的多层感知机网络能精确地表示任何 boolean 函数
多层 Sigmoid 神经元网络：有一个隐含层的多层 Sigmoid 神经元网络能以期望的精度近似任意连续函数

# 反向传播算法

举一个例子，一个网络中单独分割出一条路径：

瘦且长的网络

单独对 $W_{111}$ 求导：

$\dfrac{\delta\varphi(\theta)}{\delta W_{111}}=\dfrac{\delta\varphi(\theta)}{\delta\hat{y}}\dfrac{\delta\hat{y}}{\delta a_{L11}}\dfrac{\delta a_{L11}}{\delta h_{21}}\dfrac{\delta h_{21}}{\delta a_{21}}\dfrac{\delta a_{21}}{\delta h_{11}}\dfrac{\delta h_{11}}{\delta a_{11}}\dfrac{\delta a_{11}}{\delta W_{111}}$

对于梯度下降法，梯度的计算：

需要计算的梯度：

Gradient w.r.t output units
Gradient w.r.t hidden units
Gradient w.r.t weights and biases

# 计算损失函数对输出单元的梯度

$\nabla_{\hat{y}}\varphi(\theta)=-\frac{1}{\hat{y}_l}e_l$

其中 $e_l$ 是一个 $k$ 维向量，它的第 $l$ 个元素是 1，其他元素为 0

$\dfrac{\delta\varphi(\theta)}{\delta a_{L,i}}=-(1_{l=i}-\hat{y}_i)$

$\nabla_{a_L}\varphi(\theta)=-(e(l)-\hat{y})$

# 计算损失函数对隐含单元的梯度

$\dfrac{\delta\varphi(\theta)}{\delta h_{ij}}=(W_{i+1,.,j})^T\nabla_{a_{i+1}}\varphi(\theta)$

$\nabla_{h_i}\varphi(\theta)=(W_{i+1})^T(\nabla_{a_{i+1}}\varphi(\theta))$

$\dfrac{\delta\varphi(\theta)}{\delta a_{ij}}=\dfrac{\delta\varphi(\theta)}{\delta h_{ij}}g^\prime(a_{ij})\ [\because\ h_{ij}=g(a_{ij})]$

$\nabla_{a_i}\varphi(\theta)=\begin{bmatrix}\dfrac{\delta\varphi(\theta)}{\delta h_{i1}}g^\prime(a_{i1})\\\vdots\\\dfrac{\delta\varphi(\theta)}{\delta h_{in}}g^\prime(a_{in})\end{bmatrix}$

# 计算损失函数对参数的梯度

$\dfrac{\delta\varphi(\theta)}{\delta W_{kij}}=\dfrac{\delta\varphi(\theta)}{\delta a_{ki}}\dfrac{\delta a_{ki}}{\delta W_{kij}}=\dfrac{\delta\varphi(\theta)}{\delta a_{ki}}h_{k-1,j}$

$\nabla_{W_k}\varphi(\theta)=\nabla_{a_k}\varphi(\theta)\cdot \bold{h}_{k-1}^T$

其中加粗的 h 代表的是一个矩阵

$\dfrac{\delta\varphi(\theta)}{\delta b_{ki}}=\dfrac{\delta\varphi(\theta)}{\delta a_{ki}}\dfrac{\delta a_{ki}}{\delta b_{ki}}=\dfrac{\delta\varphi(\theta)}{\delta a_{ki}}$

$\nabla_{b_k}\varphi(\theta)=\begin{bmatrix}\dfrac{\delta\varphi(\theta)}{\delta a_{k1}}\\\dfrac{\delta\varphi(\theta)}{\delta a_{k2}}\\\vdots\\\dfrac{\delta\varphi(\theta)}{\delta a_{kn}}\end{bmatrix}=\nabla_{a_k}\varphi(\theta)$

# 算法流程：

Algorithm: gradient_descent()

$t\leftarrow 0$

$max\_iterations\leftarrow 1000;$

$\text{Initialize}\ \theta_0=[W_1^0,...,W_L^0,b_1^0,...,b_L^0]$

$\text{while t++<max\_iterations}\ do$

$h_1,h_2,...,h_{L-1},a_1,a_2,...,a_L,\hat{y}=\text{forward\_propagation}(\theta_t);$

$\nabla\theta_t=\text{backward\_propagation}(h_1,h_2,...,h_{L-1},a_1,a_2,...,a_L,y,\hat{y});$

$\theta_{t+1}\leftarrow\theta-\eta\nabla\theta_t;$

end

Algorithm: forward_propagation( $\theta$ )

$\text{for k=1 to L-1}\ do$

a_k=b_k+W_kh_

$h_k=g(a_k)$

end

a_L=b_L+W_Lh_

$\hat{y}=O(a_L);$

Algorithm: back_propagation( $h_1,h_2,...,h_{L-1},a_1,a_2,...,a_L,y,\hat{y}$ )

$\nabla_{a_L}\varphi(\theta)=-(e(y)-\hat{y});$ (计算输出层梯度)

$\text{for k=L to 1}\ do$

(计算隐藏层参数梯度)

$\nabla_{w_k}\varphi(\theta)=\nabla_{a_k}\varphi(\theta)h_{k-1}^T;$

$\nabla_{b_k}\varphi(\theta)=\nabla_{a_k}\varphi(\theta);$

(计算隐藏层输出前梯度)

$\nabla_{h_{k-1}}\varphi(\theta)=W_k^T(\nabla_{a_k}\varphi(\theta));$

$\nabla_{a_{k-1}}\varphi(\theta)=\nabla_{h_{k-1}}\varphi(\theta)\odot[...,g^\prime(a_{k-1,j}),...];$

end

# 激活函数的导数

Logistic function:
- $g(z)=\dfrac{1}{1+e^{-z}}$
- $g^\prime(z)=g(z)(1-g(z))$
tanh:
- $g(z)=\dfrac{e^z-e^{-z}}{e^z+e^{-z}}$
- $g^\prime(z)=1-(g(z))^2$

# 梯度下降及其变体

随机梯度下降算法：

	def do_stochastic_gradient_descent():
	w,b,eta,max_epochs=-2,-2,1.0,1000
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw=grad_w(w,b,x,y)
	db=grad_b(w,b,x,y)
	w-=eta*dw
	b-=eta*db

小批量梯度下降算法：

	def do_mini_batch_gradient_descent():
	w,b,eta=-2,-2,1.0
	mini_batch_size,num_points_seen=2,0
	for i in range(max_epochs):
	dw,db,num_points=0,0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	num_points_seen+=1
	if num_points_seen%mini_batch_size==0:
	w-=eta*dw
	b-=eta*db
	dw,db=0,0

动量梯度下降算法：

	def do_momentum_gradient_descent():
	w,b,eta=init_w,init_b,1.0
	prev_v_w,prev_v_b,gamma=0,0,0.9
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	v_w = gammaprev_v_w+etadw
	v_b = gammaprev_v_b+etadb
	w-=v_w
	b-=v_b
	prev_v_w=v_w
	prev_v_b=v_b

NAGD 算法：

	def do_nesterov_accelerated_gradient_descent():
	w,b,eta=init_w,init_b,1.0
	prev_v_w,prev_v_b,gamma=0,0,0.9
	for i in range(max_epochs):
	dw,db=0,0
	v_w=gamma*prev_v_w
	v_b=gamma*prev_v_b
	for x,y in zip(X,Y):
	dw+=grad_w(w-v_w,b-v_b,x,y)
	db+=grad_b(w-v_w,b-v_b,x,y)
	v_w=gammaprev_v_w+etadw
	v_b=gammaprev_v_b+etadb
	w-=v_w
	b-=v_b
	prev_v_w=v_w
	prev_v_b=v_b

Adagrad 算法：

	def do_adagrad():
	w,b,eta=init_w,init_b,0.1
	v_w,v_b,eps=0,0,1e-8
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	v_w+=dw**2
	v_b+=db**2
	w-=(eta/np.sqrt(v_w+eps))*dw
	b-=(eta/np.sqrt(v_b+eps))*db

RMSProp 算法：

	def do_rmsprop():
	w,b,eta=init_w,init_b,0,1
	v_w,v_b,eps,beta1=0,0,1e-8,0.9
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	v_w=beta1v_w+(1-beta1)dw**2
	v_b=beta1v_b+(1-beta1)db**2
	w-=(eta/np.sqrt(v_w+eps))*dw
	b-=(eta/np.sqrt(v_b+eps))*db

Adam 算法：

	def do_adam():
	w,b,eta=init_w,init_b,0.1
	m_w,m_b,v_w,v_b,m_w_hat,m_b_hat,v_w_hat,v_b_hat,eps,beta1,beta2=0,0,0,0,0,0,0,0,1e-8,0.9,0.999
	for i in range(max_epochs):
	dw,db=0,0
	for x,y in zip(X,Y):
	dw+=grad_w(w,b,x,y)
	db+=grad_b(w,b,x,y)
	m_w=beta1m_w+(1-beta1)dw
	m_b=beta1m_b+(1-beta1)db
	v_w=beta2v_w+(1-beta2)dw**2
	v_b=beta2v_b+(1-beta2)db**2
	m_w_hat=m_w/(1-math.pow(beta1,i+1))
	m_b_hat=m_b/(1-math.pow(beta1,i+1))
	v_w_hat=v_w/(1-math.pow(beta2,i+1))
	v_b_hat=v_b/(1-math.pow(beta2,i+1))
	w-=(eta/np.sqrt(v_w_hat+eps))*m_w_hat
	b-=(eta/np.sqrt(v_b_hat+eps))*m_b_hat

# 自编码器及其变体

# AutoCoder

AutoCoder

自编码器是一类特殊的前馈神经网络
Encodes 输入 $x_i$ 得到隐含表示 h
Decodes 输入 h 得到\hat
最小化特定的损失函数确保 $\hat{x_i}$ 接近与 $x_i$
当 $dim(h)<dim(x_i)$ 时，称为 under complete autocoder
- h 提取了 $x_i$ 所有重要的信息
当 $dim(h)>dim(x_i)$ 时，称为 over complete autocoder
- h 在实际中没有什么作用

线性自编码器的编码器等价于 PCA，如果满足：

使用线性编码器
使用线性解码器
使用平方根误差损失函数
对输入进行如下归一化：

$\hat{x_{ij}}=\dfrac{1}{\sqrt{m}}(x_{ij}-\dfrac{1}{m}\sum\limits_{k=1}^mx_{kj})$

# Regularization in Autoencoder

自编码器的泛化能力差，特别是对于过完备的自编码器
对于过完备的自编码器，模型会简单将 $x_i$ 复制进 h，然后再把 h 复制进\hat
为了避免较差的泛化能力，可以在目标函数中引入正则项
最简单的正则项是在目标函数中增加一个 $L_2$ -regularization 项：

$\theta=\min\limits_{W,W^*,b,c}\dfrac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^n(\hat{x}_{ij}-x_{ij})^2+\lambda\Vert\theta\Vert^2$

在使用梯度下降求解最优参数时，只需要在梯度项 $\dfrac{\delta L(\theta)}{\delta W}$ 中增加一项 $\lambda W$ (求解其他参数时，有类似的操作)
另一个方案是对编码器和解码器的权重进行捆绑 $W^*=W^T$
这种方案有效地减小了自编码器的容量，也能起到正则化的作用

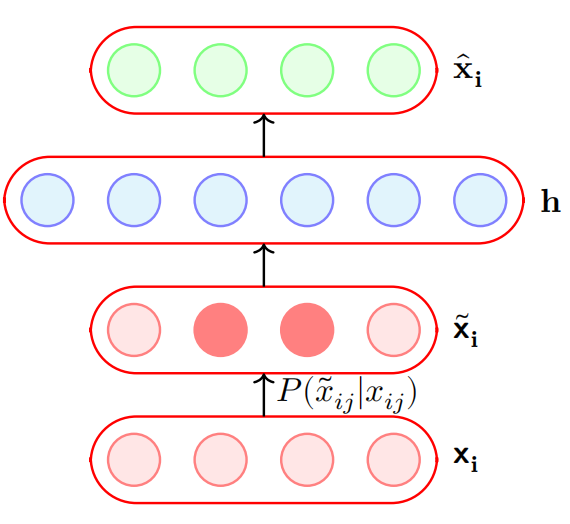
# 去噪自编码器

去噪编码器

一个去噪编码器在处理输入数里时，简单地使用一个概率分布 $(P(\tilde{x}_{ij}\vert x_{ij}))$ 对输入数据施加噪声
实际中，一个简单的概率分布 $P(\tilde{x}_{ij}\vert x_{ij})$ 可以使用下：
- $P(\tilde{x}_{ij}=0\vert x_{ij})=q$
- $P(\tilde{x}_{ij}=x_{ij}\vert x_{ij})=1-q$
以概率 q 将输入数据置成 0，以概率 (1-q) 保持原来的输入
优化的目标仍然是重构原始的输入 $x_i$

$\arg\min\limits_{\theta}\dfrac{1}{m}\sum\limits_{i=1}^m\sum\limits_{j=1}^n(\hat{x}_{ij}-x_{ij})^2$

加入噪声后，单纯复制后会导致目标函数不是最优，从而避免这种简单的复制
模型会正确地捕获输入数据的特性

# 稀疏自动编码器

隐含层经过 Sigmoid 激活后，输出结果在 0 到 1 之间
当神经元的输出接近 1，则认为神经元被激活，当输出接近 0 时，则认为该神经元没有被激活
稀疏自动编码器的目的是确保神经元在大部分时间处于非激活状态

# 收缩自编码器

收缩自编码器的设计是为了防止学习特定映射函数时，产生 overcomplete (隐藏层神经元个数大于输出神经元个数)
为了实现该目的，可以向损失函数添加一下正则项： $\Omega(\theta)=\Vert J_x(h)\Vert^2_F$ ，其中 $J_x(h)$ 是编码器的 Jacobian 矩阵
Jacobian 矩阵的 $(l,j)$ 项能够反应第 j 个输入的小变化量对第 l 个神经元的输出的影响

# 神经网络训练

# 预训练

问题：对于很深的神经网络，训练多个 epochs 后仍然不收敛
方法：
- 考虑神经网络前两层，用一个无监督的目标来训练这两层之间的权重
- 目标是要从隐含表示 ( $h_1$ ) 中重构出输入 (x)
- 经过这一步后，第一层的权重被训练，使得 $h_1$ 捕获输入 x 的重要信息
- 然后将第一层固定，在第二层上重复这一过程，然后 $h_2$ 将捕获 $h_1$ 的重要信息
- 继续这一过程，直到最后一个隐含层
- 预训练结束后，使用训练出的权重来初始化隐含层权重。所得到的的网络能够学习到输入数据类别独立的特征表示
- 预训练结束后，再在网络上增加输出层，使用特定的目标 (或损失函数) 来训练整个网络
整个过程可以理解为：先使用无监督的预训练 (无监督的目标) 来初始化网络权重，再使用特定有监督的目标来 fine tune 整个网络
正则化的作用：
- 它将权重约束到参数空间的特定区域
- L-1 regularization: 约束大多数权重为 0
- L-2 regularization: 阻止大多数权重取值较大
- 预训练将权重约束到参数空间的特定区域，将权重约束到能很好捕获数据特性的区域

# 激活函数

问题：Sigmoid 神经元容易很快达到饱和，导致梯度消失 (Sigmoid 神经元不是 0 中心化的)
ReLU 神经元：学习率过高会导致大部分 ReLU 神经元死亡
ReLU 神经元变体：
- Leaky ReLU
- Maxout
- ELU
记忆点：
- Sigmoid 激活函数效果不好
- ReLU 是 CNN 的标准激活函数
- 可以尝试 Leaky ReLU/Maxout/ELU
- tanh 和 Sigmoids 仍然在 LSTMs/RNNs 中使用

# 块归一化

如果每一层的预激活服从单位高斯分布，对输入的变化会更鲁棒
可以对每一层预激活进行如下 "标准化" 操作：

$\hat{s_{ik}}=\dfrac{s_{ik}-E\vert s_{ik}\vert}{\sqrt{var(s_{ik})}}$

用小批量的数据计算 $E[s_{ik}]$ 和 $Var[s_{ik}]$
因此，确保不同层的输入的分布不会随着 batch 的不同而改变
该操作称为 Batch Normalization

# Dropout

在神经网络中，移除一个结点和与之相连的边，会得到一个瘦身的网路
Dropout 本质上可以看作是对隐含单元施加噪声
阻止隐含单元互相适，一个隐含单元不能过于依赖其他隐含单元 (因为其他隐含单元可能被移除)
每个隐含单元必须学习到对其他隐含单元的移除足够鲁棒
Dropout 提高了网络的冗余性和鲁棒性

# 卷积神经网络

# 卷积

对于 1D 的输入，使用一个 1D 的滤波器在其上面滑动
对于 @D 的输入，使用一个 @D 的滤波器在其上面滑动

卷积计算：

Padding：P (扩展大小)
Stride：S (移动步长)
Kernel_Size：F (卷积核大小)
Map_Size: W (输入图片大小)
OutputMap_Size: $\dfrac{W-F+2P}{S}+1$

通道数取决于输入通道数以及卷积核的个数

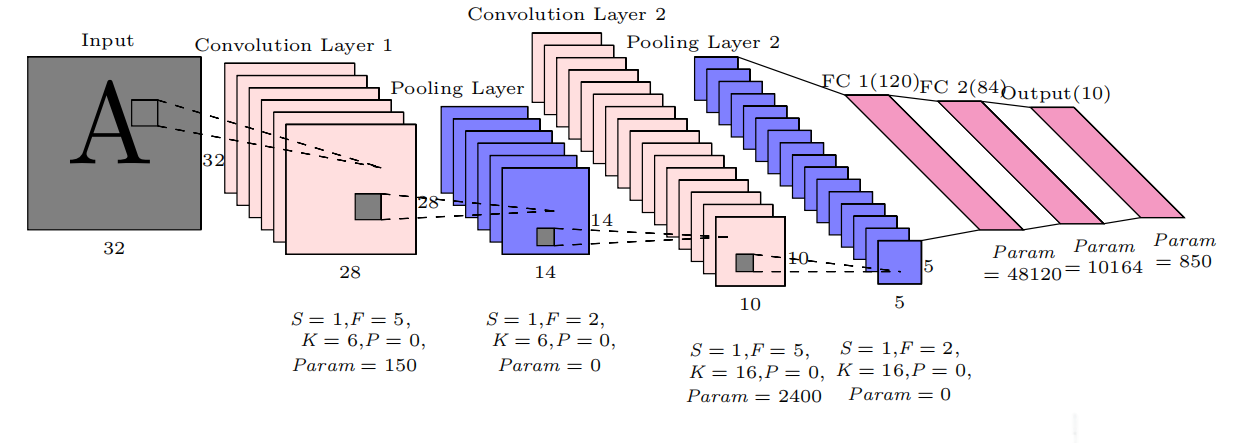
例子：

卷积例子

经典卷积网络：

AlexNet
ZFNet
VGGNet
GoogleNet
ResNet

深度学习复习笔记