形式语言复习四

形式语言复习四

# 正则表达式

# RE 的定义

正则表达式

• $\phi$ 是$\Sigma$ 上的 RE，它表示语言$\phi$

• $\epsilon$ 是$\Sigma$ 上的 RE，它表示语言 {$\epsilon$}

• 对于$\forall a\in\Sigma,a$ 是$\Sigma$ 上的 RE，它表示语言 {$a$}

• 如果 r 和 s 分别是$\Sigma$ 上表示语言 R 和 S 的 RE，则：

  • r 与 s 的 "和"(r+s) 是$\Sigma$ 上的 RE，(r+s) 表达的语言为$R\cup S$
  • r 与 s 的 "乘积"(rs) 是$\Sigma$ 上的 RE，(rs) 表达的语言为$RS$
  • r 的克林闭包 ($r^*$) 是$\Sigma$，($r^*$) 表达的语言为$R^*$

• 只有满足以上四条的才是$\Sigma$ 的才是$\Sigma$ 上的 RE

约定：

• r 的正闭包$r^+$ 表示 r 与 ($r^*$) 的乘积以及 ($r^*$) 与 r 的乘积：$r^+=(r(r^*))=((r^*)r)$
• 闭包运算的优先级最高，乘运算的优先级次之，加运算的优先级最低
• 意义明确时，RE r 表示的语言记为 L (r), 也可以直接地记为 r
• 加、乘、闭包运算均执行左结合规则

相等：

• r,s 是字母表$\Sigma$ 上的一个 RE，如果 L (r)=L (s)，则称 r 与 s 相等，记作 r=s
• 相等也称为等价

基本结论：

• 结合律：(rs) t=r (st),(r+s)+t=r+(s+t)

• 分配率：r (s+t)=rs+rt,(s+t) r=sr+tr

• 交换律：r+s=s+r

• 幂等律：r+r=r

• 加法运算零元素：$r+\phi=r$

• 乘法运算单位元：$r\epsilon=\epsilon r=r$

• 乘法运算零元素：$r\phi=\phi r=\phi$

• $L(\phi)=\phi,L(\epsilon)=\epsilon,L(a)=a$

• $L(rs)=L(r)L(s),L(r+s)=L(r)\cup L(s)$

• $L(r^*)=(L(r))^*$，$L(\phi^*)=${$\epsilon$}

• $L((r+\epsilon)^*)=L(r^*),L((r^*)^*)=L(r^*),L((r^*s^*)^*)=L((r+s)^*)$

• 如果$L(r)\subseteq L(s)$，则$r+s=s$

• $L(r^n)=(L(r))^n$

• $r^nr^m=r^{n+m}$，一般地，$r+\epsilon\neq r,(rs)^n\neq r^ns^n,rs\neq sr$

幂：

• r 是字母表$\Sigma$ 上的 RE，r 的 n 次幂定义为：
  • $r^0=\epsilon$
  • $r^n=r^{n-1}r$

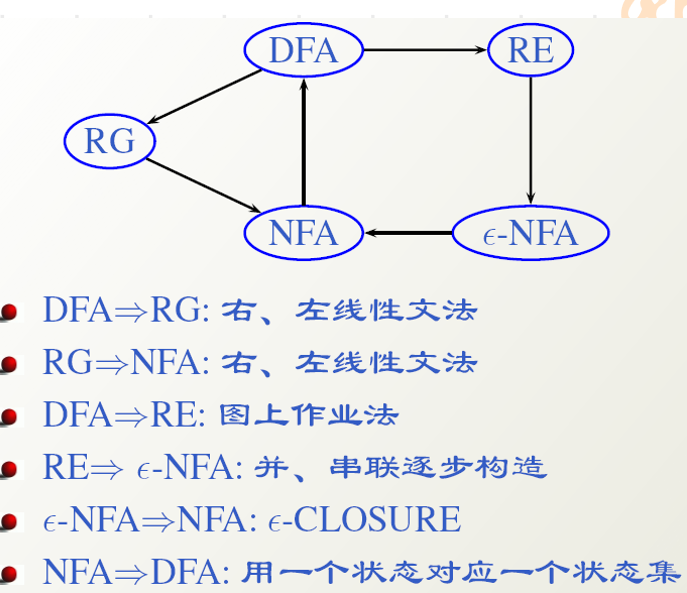
# RE 与 FA 等价

正则表达式 r 称为与 FA M 等价，如果 L (r)=L (M)

• 从开始状态出发，根据状态之间按照转移所确定的后继关系，依次计算出所给 FA 的各个状态 q 对应的 set (q)，并且最终得到相应的 FA 接受的语言的 RE 表示

定理：RE 表示的语言是 RL

# RL 可以用 RE 表示

定理：RL 可以用 RE 表示

• 图上作业法操作步骤：

  • 预处理

    • 用标记为 X 和 Y 的状态将 M"括起来"：

      在状态转移图中增加标记为 X 和 Y 的状态，从标记为 X 的状态到标记为$q_0$ 的状态引一条标记为$\epsilon$ 的弧；从标记为$q(q\in F)$ 的状态到标记为 Y 的状态分别引一条标记为$\epsilon$ 的弧

    • 去掉所有的不可达状态

  • 通过对预处理得到的状态转移图重复如下操作，直到该图不再包含除了标记为 X 和 Y 外的其他状态，并且这两个状态之间最多只有一条弧

    • 并弧
      • 将从 q 到 p 的标记为$r_1,r_2,...,r_g$ 并行弧用从 q 到 p 的，标记为$r_1+r_2+...+r_g$ 的弧取代这 g 个并行弧
    • 去状态 1
      • 如果从 q 到 p 有一条标记为$r_1$ 的弧，从 p 到 t 有一条标记为$r_2$ 的弧，不存在从状态 p 到状态 p 的弧，将状态 p 和与之关联的这两条弧去掉，用一条 q 到 t 的标记为$r_1r_2$ 的弧代替
    • 去状态 2
      • 如果从 q 到 p 有一条标记为$r_1$ 的弧，从 p 到 t 有一条标记为$r_2$ 的弧，从状态 p 到状态 p 标记为$r_3$ 的弧，将状态 p 和与之关联的这三条弧去掉，用一条 q 到 t 的标记为$r_1r_3^*r_2$ 的弧代替
    • 去状态 3
      • 如果图中只有三个状态，而且不存在从标记 X 的状态到达标记为 Y 的状态的路，则将除标记为 X 的状态和标记为 Y 的状态之外的第 3 个状态及其相关的弧全部删除

  • 从标记 X 的状态到标记为 Y 的状态的弧的标记为所求的正则表达式。如果此弧不存在，则所求正则表达式为$\phi$

推论：正则表达式与 FA，正则文法等价，是正则语言的表示模型

# 正则语言等价模型总结