首页 计算机科学 计算机组成原理

# 进制转换

基数：每个数码位所用到的不同符号的个数，r 进制的基数为 r

二进制：

  • 可以使用两个稳定状态的物理器件表示
  • 0,1 正好对应逻辑值假、真。方便实现逻辑运算
  • 可很方便地使用逻辑门电路实现算术运算

任意进制 -> 十进制：

  • 二进制：10010010.110→1∗27+1∗24+1∗2−1+1∗2−2=146.7510010010.110\rightarrow1*2^7+1*2^4+1*2^{-1}+1*2^{-2}=146.75
  • 八进制：251.5→2∗82+5∗81+5∗8−1=168.625251.5\rightarrow 2*8^2+5*8^1+5*8^{-1}=168.625
  • 十六进制：AE86.1→10∗163+14∗162+8∗161+6∗160+1∗16−1=44678.0625AE86.1\rightarrow 10*16^3+14*16^2+8*16^1+6*16^0+1*16^{-1}=44678.0625

二进制 -> 八进制、十六进制

  • 二进制 -> 八进制
    • 三位一组，转换成对应八进制符号
    • 111100010.01101->(001)(111)(000)(010).(011)(010)->1702.32 (八进制)
    • 同理八进制 -> 二进制时，一位对应三位
  • 二进制 -> 十六进制
    • 四位一组，转换成对应十六进制符号
    • 111100010.01101->(0011)(1100)(0010).(0110)(1000)->3C2.68 (十六进制)
    • 同理十六进制 -> 二进制时，一位对应四位

各种进制常见书写形式：

  • 二进制 ——(1001101)2,1001110B(1001101)_2,1001110B

  • 八进制 ——(1632)8(1632)_8

  • 十六进制 ——(1652)16,1652H,0×1652(1652)_{16},1652H,0\times1652

  • 十进制 ——(1652)10,1652D(1652)_{10},1652D

十进制 -> 任意进制：

  • 对于整数部分，除基取余法，先取得的 "余" 是整数的低位

  • 对于小数部分，乘积取余法，先取得的 "整" 是小数的高位

  • 有的十进制小数无法对二进制精确表示，如：0.3

# 真值和机器数

真值：符合人类习惯的数字

机器数：数字实际存到机器里的形式，正负号需要被数字化

# BCD 码

每四个二进制位表示一个十进制字符

8421 码 (有权码)：

  • 正常的二进制对应映射

  • 十进制 5+8-> 二进制 0101+1000-> 机器计算：先进行二进制加法，当得出的数字结果在 1010~10010 时，对整体加 6，即加 0110

  • 若相加结果在合法范围内，则无需修正

余 3 码 (无权码，每一个二进制位无固定权值)：

  • 8421 码 +(0011)2(0011)_2

2421 码：改变权值定义

  • 表示 0-4 时，最高位为 0，表示 5-9 时，最高位为 1

# 无符号整数的表示和运算

无符号整数，即 "自然数"

  • 全部二进制位都是数值位，没有符号位，第 i 位的位权是2^
  • n bit 无符号整数表示范围 0~2n−12^n-1，超出则溢出，意味着该计算机无法一次处理这么多
  • 可以表示最小的数全 0，可以表示最大的数全 1

加法运算：从最低位开始，按位相加，并往更高位进位

减法运算：

  • 被减数不变，减数全部位按位取反、末尾 + 1，减法变加法
  • 从最低位开始，按位相加，并往更高位进位

# 带符号整数

带符号整数，即整数

原码：最高位为符号位，其他位为数值位

  • 符号位 0/1 对应正 / 负，剩余的数值位表示真值的绝对值

  • 若机器字长为 n+1 位，带符号整数的原码表示范围：−(2n−1)≤x≤2n−1-(2^n-1)\le x\le 2^n-1

  • 真值 0 有两种形式：+0 和 - 0，[+0] (原)=0.0000000，[-0] (原)=1.0000000

原码缺点：符号位不能参与运算，需要设计复杂的硬件电路才能处理

补码表示真值 —— 符号位可以参与计算

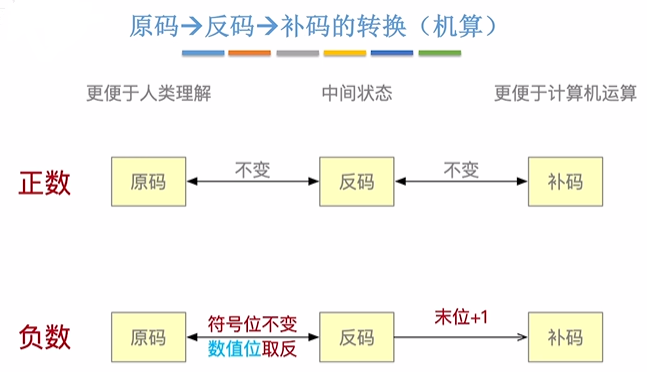
不同码转换

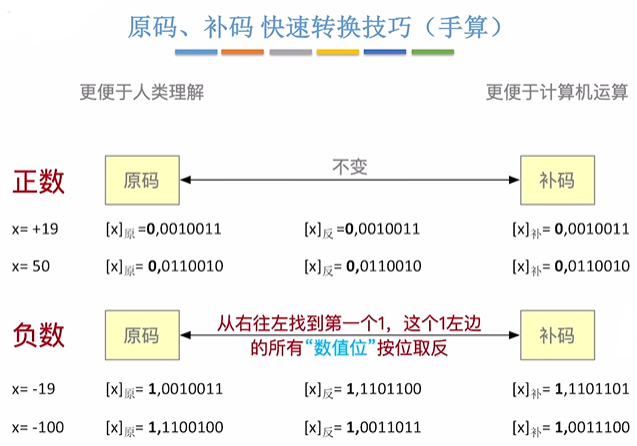
补码原码转换

补码的加法：

  • 从最低位开始，按位相加 (符号位参与运算)，并往更高位进位

  • 注意：

    • 补码的数值位不能解读为 "位权"

补码的减法：

  • A-B=A+(-B)，因此，将 B 转变成 - B 即可
  • 从 [B] (补)<->[-B] (补)，需要全部按位取反、末位加 1

无符号整数的减法：

  • 被减数不变，减数全部按位取反，末位加 1，减法变加法
  • 从最低位开始，按位相加，并往更高位进位

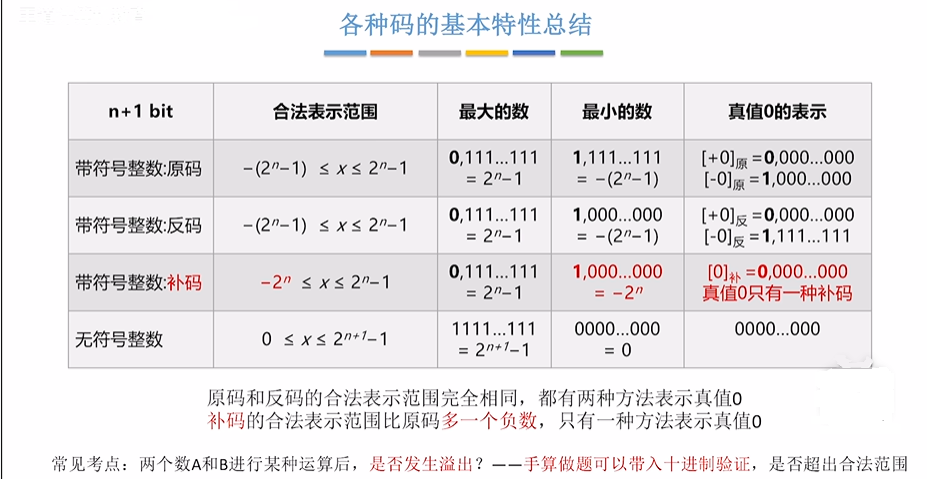
各种码基本特性

移码：补码的基础上符号位取反。注意：移码只能用于表示整数

  • 真值 0 只有一种表示方法：1000000

  • 机器字长为 n+1 位，移码整数的表示范围：−2n≤x≤2n−1-2^n\le x \le 2^n-1（与补码相同）

  • 移码表示的整数很方便用硬件电路对比大小

原码和反码的合法表示范围完全相同，都有两种方法表示 0

补码的合法表示范围比原码多一个负数，只有一种方法表示 0

移码的合法表示范围比原码多一个负数，只有一种方法表示 0

# 定点小数

定点整数（小数点默认在数值部分后面）的编码表示：原码、反码、补码、移码

定点小数（小数点默认在符号位后面）的编码表示：原码、反码、补码

定点小数原 / 反 / 补码的转换与整数一样

定点小数的加 / 减运算：

  • 对于两个定点小数 A，B 进行加减法时，需先转换为补码
  • 加法：
    • 从最低位开始，按位相加 (符号位参与计算)，并往更高维进位
  • 减法：
    • 被减数不变，减数全部按位取反，末位 + 1，加法变减法
    • 从最低位开始，按位相加，并往更高位进位

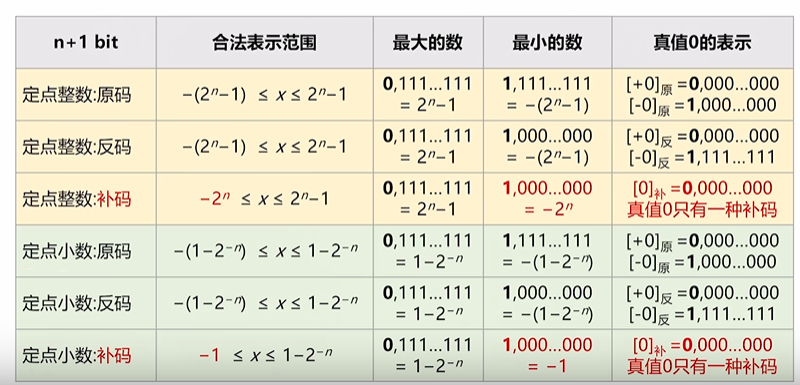
定点小数比较

特别注意：定点整数和定点小数位数扩展时，拓展位置不一样